1. Basic Facts about the Gamma Function
The Gamma function is defined by the improper integral
| Gamma(x) = INT_{0}^{INFTY}[t^{x} e^{-t} {dt}/{t} ] . |
The integral is absolutely convergent for x >= 1 since
| t^{x-1} e^{-t} <= e^{-t/2} , t ≫ 1 |
and INT_{0}^{INFTY}[e^{-t/2} dt ] is convergent. The preceding inequality is valid, in fact, for all x. But for x < 1 the integrand becomes infinitely large as t approaches 0 through positive values. Nonetheless, the limit
| lim_{r --> 0+} INT_{r}^{1}[t^{x-1} e^{-t} dt ] |
exists for x > 0 since
| t^{x-1} e^{-t} <= t^{x-1} |
for t > 0, and, therefore, the limiting value of the preceding integral is no larger than that of
| lim_{r --> 0+} INT_{r}^{1}[t^{x-1} dt ] = {1}/{x} . |
Hence, Gamma(x) is defined by the first formula above for all values x > 0 .
If one integrates by parts the integral
| Gamma(x + 1) = INT_{0}^{INFTY}[t^{x} e^{-t} dt ] , |
writing
| INT_{0}^{INFTY}[udv ] = u(INFTY)v(INFTY) - u(0)v(0) - INT_{0}^{INFTY}[vdu ] , |
with dv = e^{-t}dt and u = t^{x}, one obtains the functional equation
| Gamma(x+1) = x Gamma(x) , x > 0 . |
Obviously, Gamma(1) = INT_{0}^{INFTY}[e^{-t} dt ] = 1 , and, therefore, Gamma(2) = 1 · Gamma(1) = 1, Gamma(3) = 2 · Gamma(2) = 2!, Gamma(4) = 3 Gamma(3) = 3!, …, and, finally,
| Gamma(n+1) = n! |
for each integer n > 0.
Thus, the gamma function provides a way of giving a meaning to the “factorial” of any positive real number.
Another reason for interest in the gamma function is its relation to integrals that arise in the study of probability. The graph of the function varphi defined by
| varphi(x) = e^{-x^{2}} |
is the famous “bell-shaped curve” of probability theory. It can be shown that the anti-derivatives of varphi are not expressible in terms of elementary functions. On the other hand,
| Phi(x) = INT_{-INFTY}^{x}[varphi(t) dt ] |
is, by the fundamental theorem of calculus, an anti-derivative of varphi, and information about its values is useful. One finds that
| Phi(INFTY) = INT_{-INFTY}^{INFTY}[e^{-t^{2}} dt ] = Gamma(1/2) |
by observing that
| INT_{-INFTY}^{INFTY}[e^{-t^{2}} dt ] = 2 · INT_{0}^{INFTY}[e^{-t^{2}} dt ] , |
and that upon making the substitution t = u^{1/2} in the latter integral, one obtains Gamma(1/2).
To have some idea of the size of Gamma(1/2), it will be useful to consider the qualitative nature of the graph of Gamma(x). For that one wants to know the derivative of Gamma.
By definition Gamma(x) is an integral (a definite integral with respect to the dummy variable t) of a function of x and t. Intuition suggests that one ought to be able to find the derivative of Gamma(x) by taking the integral (with respect to t) of the derivative with respect to x of the integrand. Unfortunately, there are examples where this fails to be correct; on the other hand, it is correct in most situations where one is inclined to do it. The methods required to justify “differentiation under the integral sign” will be regarded as slightly beyond the scope of this course. A similar stance will be adopted also for differentiation of the sum of a convergent infinite series.
Since
| {d}/{dx} t^{x} = t^{x}(log t) , |
one finds
| {d}/{dx} Gamma(x) = INT_{0}^{INFTY}[t^{x} (log t) e^{-t} {dt}/{t} ] , |
and, differentiating again,
| {d^{2}}/{dx^{2}} Gamma(x) = INT_{0}^{INFTY}[t^{x} (log t)^{2} e^{-t} {dt}/{t} ] . |
One observes that in the integrals for both Gamma and the second derivative Gamma^{″} the integrand is always positive. Consequently, one has Gamma(x) > 0 and Gamma^{″}(x) > 0 for all x > 0. This means that the derivative Gamma^{′} of Gamma is a strictly increasing function; one would like to know where it becomes positive.
If one differentiates the functional equation
| Gamma(x+1) = x Gamma(x) , x > 0 , |
one finds
| psi(x+1) = {1}/{x} + psi(x) , x > 0 , |
where
| psi(x) = {d}/{dx} logGamma(x) = {Gamma^{′}(x)}/{Gamma(x)} , |
and, consequently,
| psi(n+1) = psi(1) + SUM_{k = 0}^{n}[{1}/{k} ] . |
Since the harmonic series diverges, its partial sum in the foregoing line approaches INFTY as x --> INFTY. Inasmuch as Gamma^{′}(x) = psi(x)Gamma(x), it is clear that Gamma^{′} approaches INFTY as x --> INFTY since Gamma^{′} is steadily increasing and its integer values (n-1)!psi(n) approach INFTY. Because 2 = Gamma(3) > 1 = Gamma(2), it follows that Gamma^{′} cannot be negative everywhere in the interval 2 <= x <= 3, and, therefore, since Gamma^{′} is increasing, Gamma^{′} must be always positive for x >= 3. As a result, Gamma must be increasing for x >= 3, and, since Gamma(n + 1) = n!, one sees that Gamma(x) approaches INFTY as x --> INFTY.
It is also the case that Gamma(x) approaches INFTY as x --> 0. To see the convergence one observes that the integral from 0 to INFTY defining Gamma(x) is greater than the integral from 0 to 1 of the same integrand. Since e^{-t} >= 1/e for 0 <= t <= 1, one has
| Gamma(x)>INT_{0}^{1}[(1/e)t^{x-1}dt] = (1/e) |
| _{t = 0}^{t = 1} = {1}/{ex} . |
It then follows from the mean value theorem combined with the fact that Gamma^{′} always increases that Gamma^{′}(x) approaches -INFTY as x --> 0.
Hence, there is a unique number c > 0 for which Gamma^{′}(c) = 0, and Gamma decreases steadily from INFTY to the minimum value Gamma(c) as x varies from 0 to c and then increases to INFTY as x varies from c to INFTY. Since Gamma(1) = 1 = Gamma(2), the number c must lie in the interval from 1 to 2 and the minimum value Gamma(c) must be less than 1.
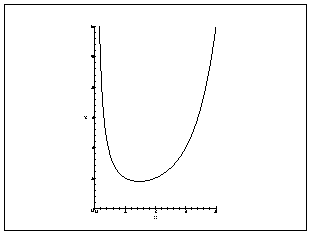
Figure 1: Graph of the Gamma Function |
Thus, the graph of Gamma (see Figure 1) is concave upward and lies entirely in the first quadrant of the plane. It has the y-axis as a vertical asymptote. It falls steadily for 0 < x < c to a postive minimum value Gamma(c) < 1. For x > c the graph rises rapidly.